相似と合同とその書き方 相似は、2つの図形の形がまったく同じであれば 何倍に拡大・縮小されていても相似ですし 回転・反転していても相似となります。 また、「相似」かつ「大きさも同じ(1倍)」のとき「2つの図形は合同である」と言います。 相似について記述するときは、 対応し当然「相似の中心o 「高さにあたるもの」「底辺にあたるもの」の考え方は 相似でなくても、相似でも使える 「あたるもの」は「相似比の2乗は面積比」の考え方をカバーする 「高さにあたるもの」 ×「底辺にあたるもの」 「相似比の2乗は面積比」 体積比でも同様に考えることができます7 モニン・オブコフの相似則 の値は小さくなる。関数 M の形は実験によって求められる。いくつかの実 験式が提案されているが、ここでは最も簡単な例を示す。安定成層の場合、 M=1 7 ( 0 ) 14 不安定成層の場合、 M= 1−16 −1/4 ( 0 ) 15 ただし、 = z L 16 14を13に代入して、境界条件を
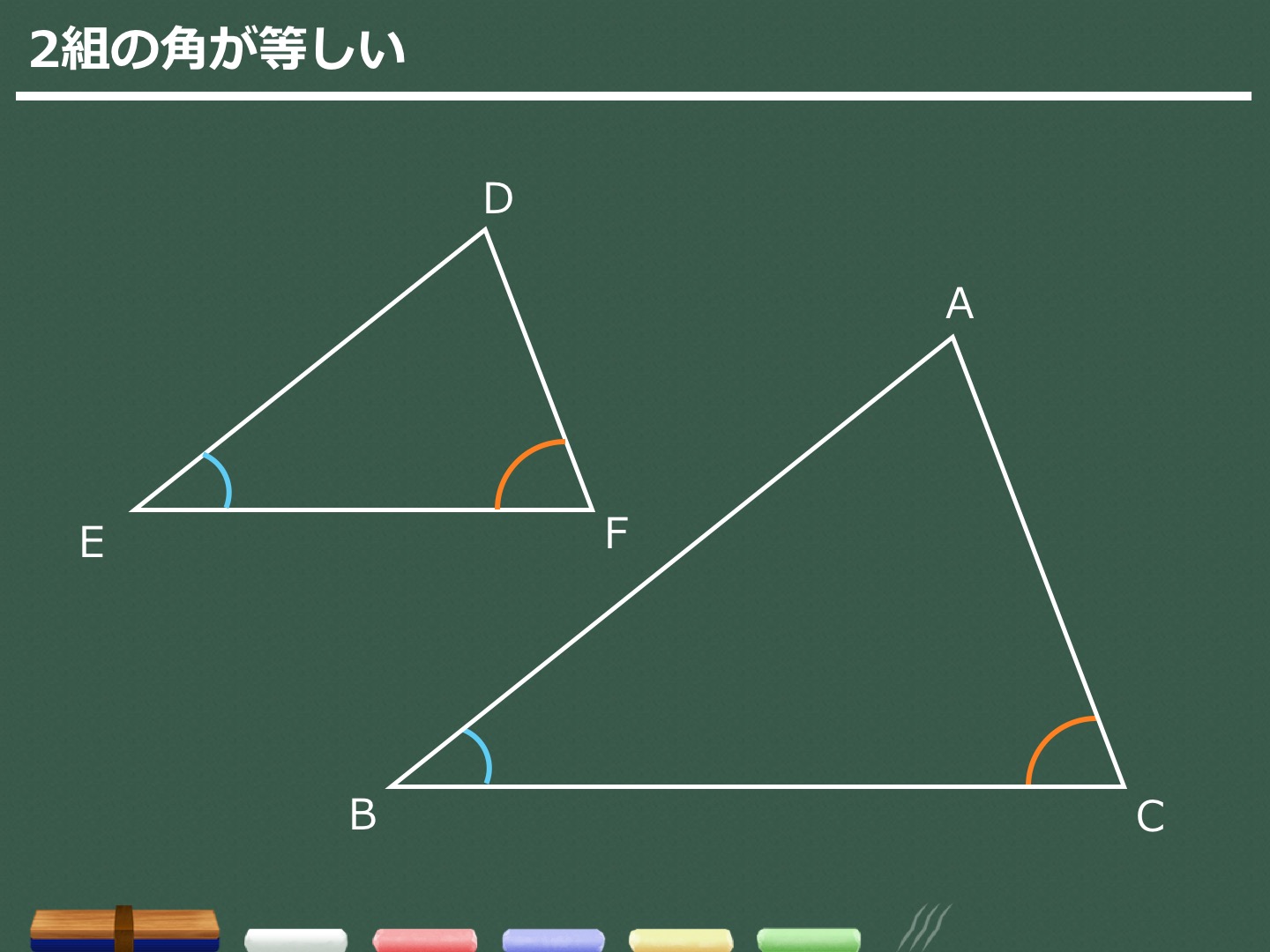
3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
相似の中心 求め方
相似の中心 求め方- 3分で分かる!中心角の求め方ー公式とその証明、練習問題をわかりやすく 数学 数学対策今すぐ使える公式講座!パターン学習 数学 812 3分で分かる!方べきの定理の証明・使い方 数学 3分で分かる!約数の個数円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45° xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135° 2 135 ° 2 = 675° 同様に、yは2コマ分の中心角の半分 → y = 1 2 1 2 (2×45°) = 90° 2 90 ° 2 = 45° 同じ弧より




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
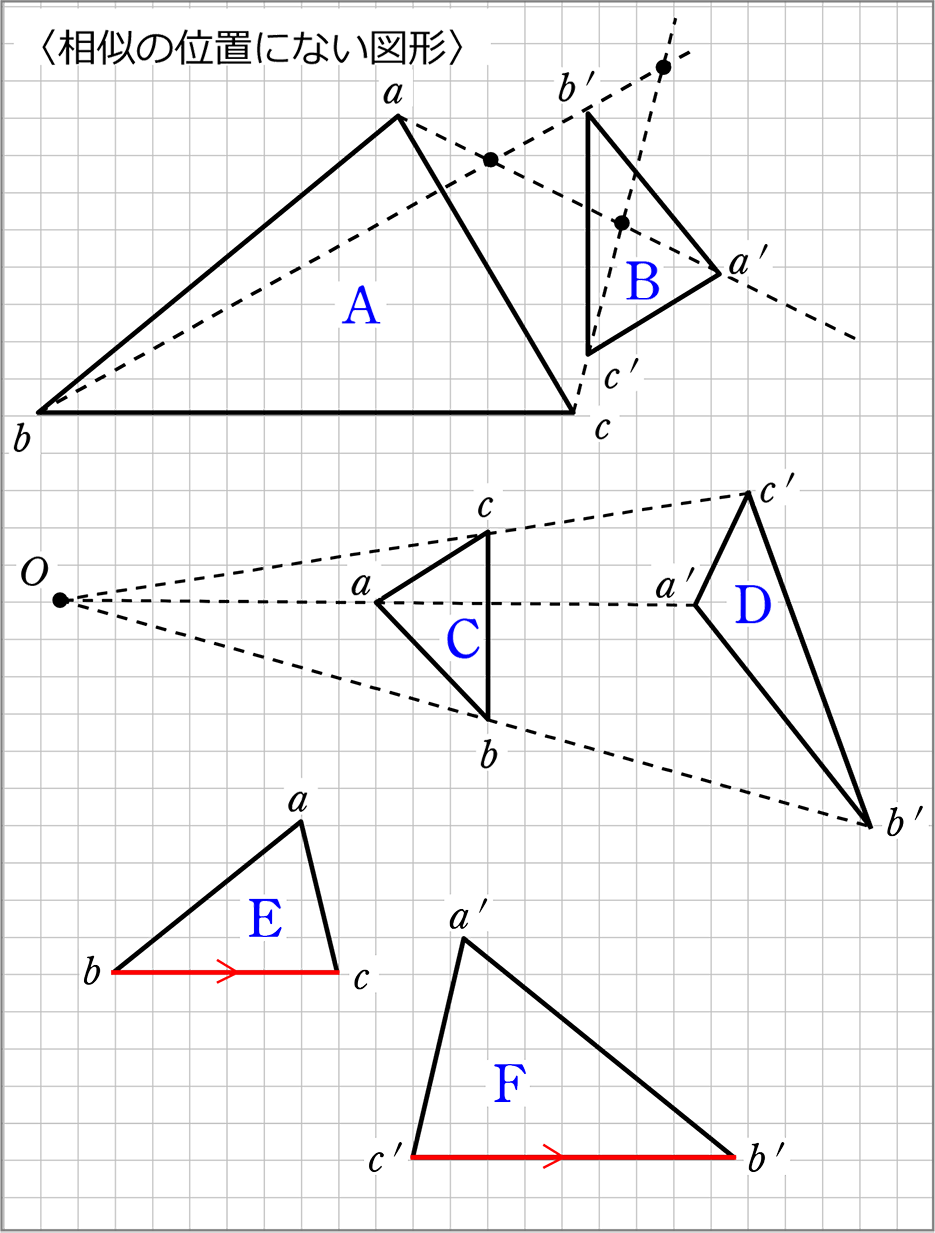
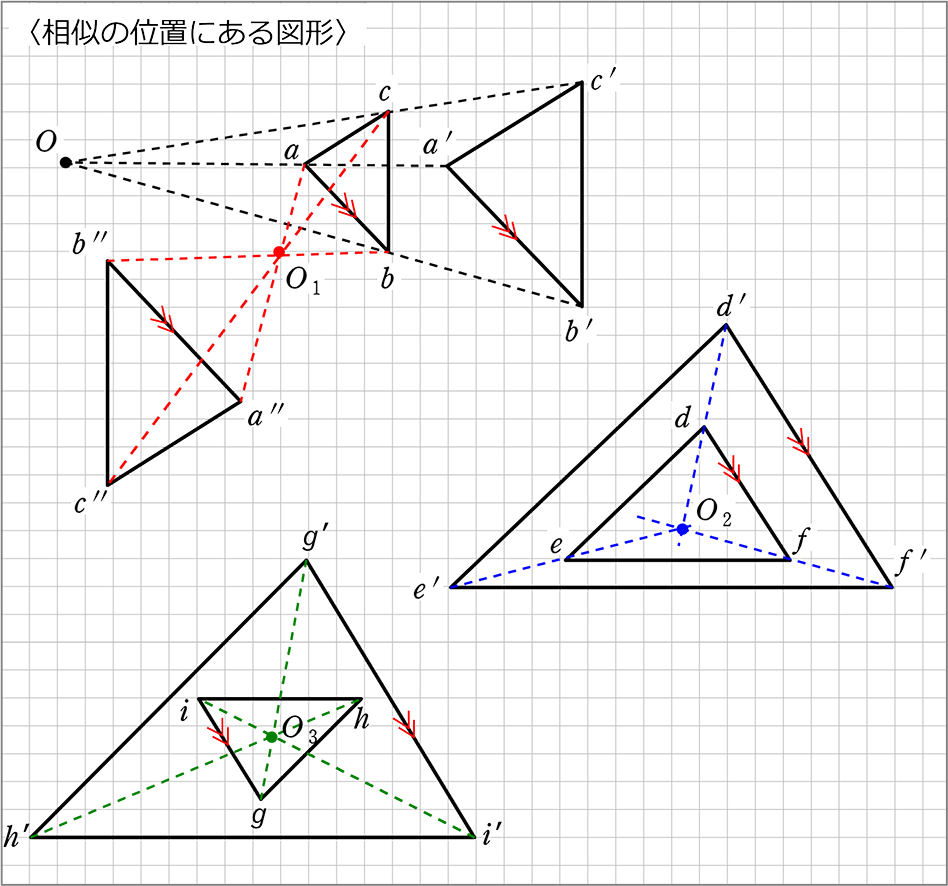
②比を求めたい場合は、比を求めたい直線を、1辺として持つ三角形を見つける ③それと相似な図形を探し、相似比を出す 基本的にはこの流れで相似の問題は解いていきます。 応用の問題でも最初の流れは同じです。特に①と②は機械的にできること相似の中心,相似の位置 相似な図形の対応する点どうしを結ぶ直線が1点で交わり、その点から対応する点までの距離の比がすべて等しいとき、その点を 相似の中心 とよぶ。中心に回転すると、2つの図形を重ね合わせることができる. 不動点の位置を作図する方法は,一般的にはコンパスと定規で求められる.正方形の各頂点を a,b,c,d , 移動後の正方形の頂点を a',b',c',d' としたとき,線分 aa' の垂直二等分線と,線分 bb' の垂直
1. 1次変換(線形変換)とは (1) 写像のうちで同一集合から同一集合への対応となっているものを 変換 といいます. (2) 平面上の点 (x, y) を点 (x', y' ) に移す変換 f が次の式で表されるとき,この変換 f を 1次変換(線形変換) という. f x'=axby ・・・① 相似とは2つの図形の片方を縮小・拡大して、平行移動、回転移動、対称移動を行えばもう片方の図形と重なる関係のことを言います。 つまり、 2つの図形の形が同じであれば相似 であると 円の中心の求め方 数学 ケガキについて 工学 4 ミリのステンレスに穴を開けたい diy・エクステリア 5 作図により円の中心の求める方法について質問です。 ①ある円で任意の異なる4点a,b,c,dをとる。 数学 6 製図上の"r"について その他(ソフトウェア) 7 弧から、中心点を求め
ある相似比27の三角錐では、体積比はいくつになるでしょうか。 解答 上述のように、体積比の求め方は辺の長さの比を3乗すればいいので、2^3:7^3=8:343と変換されました。 今度は逆に体積比から辺の長さの比を求めていきましょう 例題 円の中心間距離の求め方 まずはじめに行うのが、円の中心点からもう一方の円の中心点までの距離を調べ、その距離と2円の半径の関係を比べることです。 具体的には、2つの円の中心点の座標から三平方の定理を使って中心点どうしの距離を求めます。 <三平方の定理でdを求める> 半径相似な図形の見つけ方、相似条件とは?←今回の記事 平行線と比の利用、辺の長さを求める問題をパターン別解説! 木の高さを求める方法について解説! 中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比




中3数学 拡大図 縮図の作図 映像授業のtry It トライイット
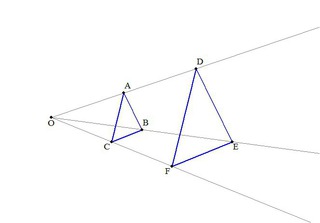



中学校数学 3年生 図形 相似な図形 Wikibooks
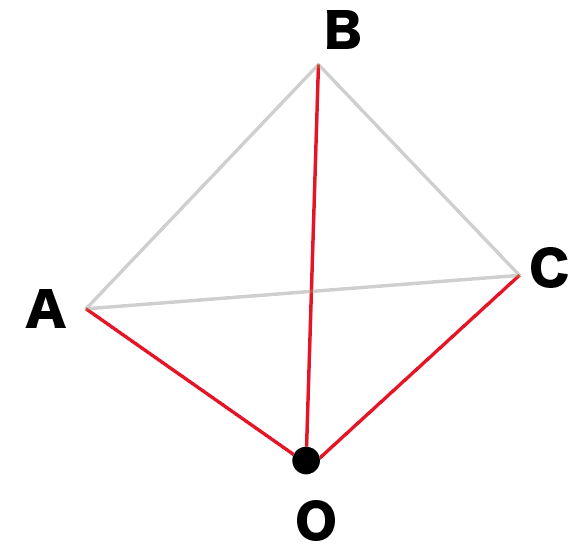
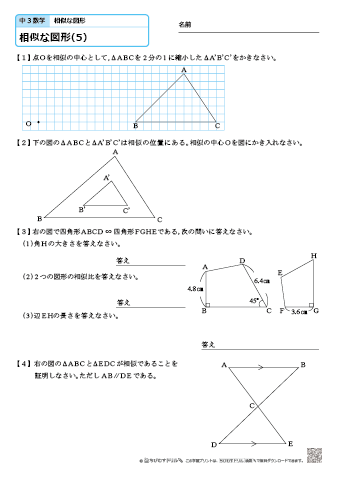
以上の区別が付けられるようになればOKです! 終わりです~。 図形のこと ベクトル 中3数学 図形の性質 よかったらシェアしてね! URL Copied! 目次 使う定理・法則 三平方の定理 円周角の定理 三角形の相似条件 外接円の半径の求め方 例題 まとめ 使う定理・法則 三平方の定理 wiki参照 三平方の定理とは、直角三角形の斜辺と 他の二辺の間に成り立つ超 読者になる ジャムと愉快な仲間たち(0名) ジャムが数学とかを熱く語ります。相似1 四角形ABCDと四角形EFGHは相似の位置にある。このとき相似の中心Oを求めなさい。 a b c d e f g h 相似な三角形を記号∽を
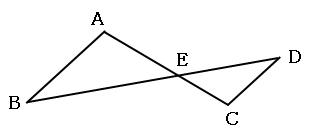



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名
『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いのでBの長さを求めてください。 相似比が1:4と分かっているので簡単です。辺の長さを4倍すればBの辺の長さになります。よって2cm×4=8cmです。 スポンサーリンク 相似比と面積比の関係、違い 相似比と面積比の違いを下記に示します。 相似比(そうじひ) ⇒ 相似な図形における辺の長さの比相似な図形や中心の作図中3数学 問題をノーヒントでやってみよう 答えをチェックしよう 授業動画をご覧くださいませ。 攻略ポイントを確認しよう ・平行線の同位角、平行線の錯角は等しい ・同位角や錯角が等しければ、2本の直線は平行である
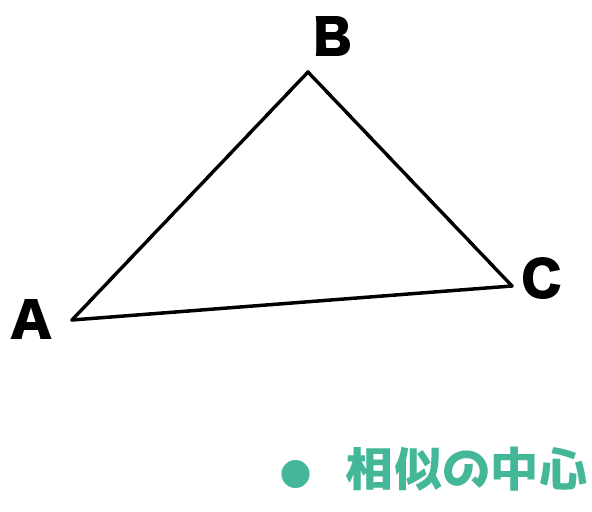



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
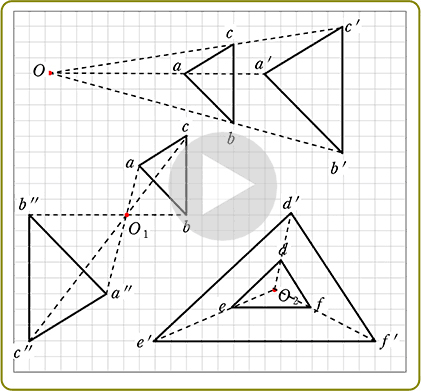



中学数学 図形の相似
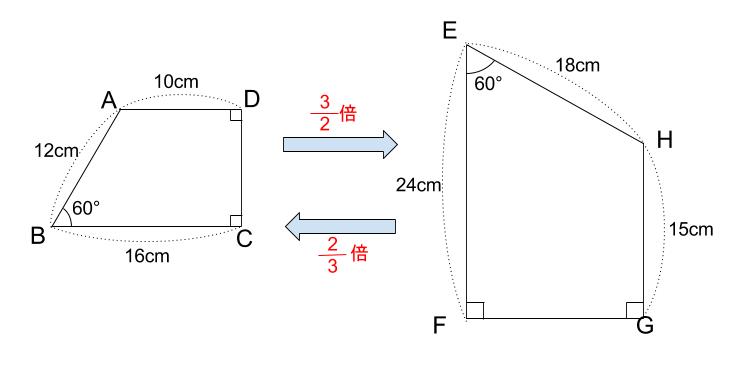
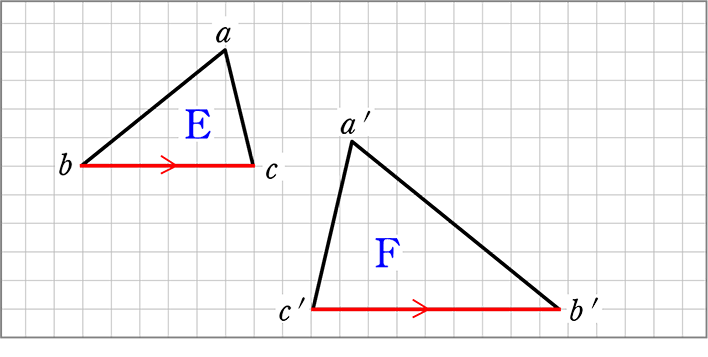
相似の中心の求め方。 y=3(x1)^22(i) y=5(x2)^23(ii) 頂点は (i)P(1、2) (ii)Q(2、3) 相似の中心R(x、y) 相似比は(i)(ii)=53 RPRQ=53 よって内分の公式より ・(2x3×1)/(32)=2 ・(2y3×2)/(32)=3 以上より R(7/2、9/2) であってますか? 外分の公式はわかるのですが使い方がただし,(*3)の方が「相似比」に対応しており,面積比の問題への応用が楽なので(*3)の方が有利だと考えられます.(筆者の手元にある中学校の教科書はいずれも(*3)の形で書かれています) 要点 辺の比は (こっちの図形)(あっちの図形) aa'=bb' (*3) の順に並べるのが標準的 相似関係の2つの台形の高さがそれぞれx、Lで、底辺はどちらもdであるとき、高さがxのとき台形の上辺はdx = (dLd)x/L dになると本に書いてあったのですが証明方法が解りません・・・証明方法を教えてください。相似関係であることが関
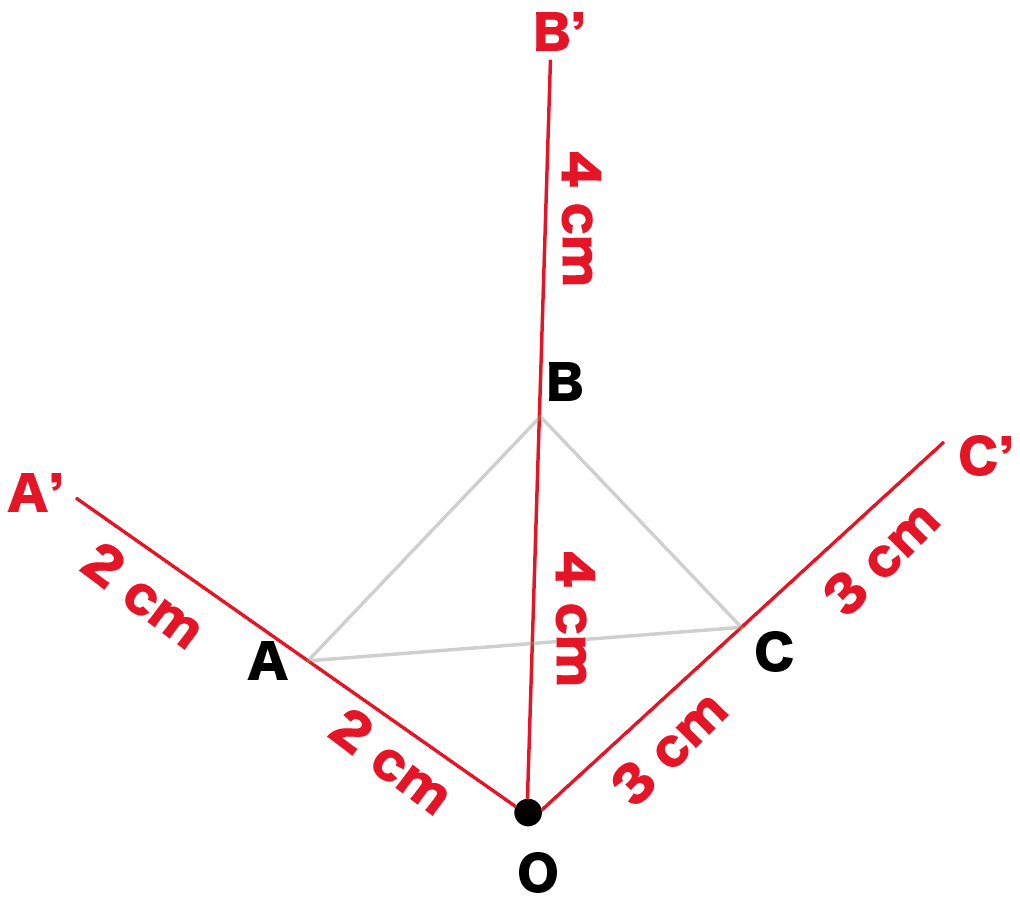



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



Http Www Rs Tottori U Ac Jp Mathedu Mathedu Journal17 Files 17 01 Pdf
直角三角形の相似 相似の証明でも取り扱った「直角三角形の相似」です。 このページでは辺の長さや比を求めていきましょう。 相似な直角三角形が現れる図形として、最重要・最頻出のものを扱います! 直角である頂点から斜辺へ垂線を まずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 少し大きめの半円を書くよ 周上の他の場所にも、コンパスの針を置いて さっきと同じ大きさの半円を書くよ そして、半円2つが重なった2点を結ぶ線を引くよ 最後に、もう1つ他の周上に 場合の数の求め方~袋から球を取り出すときの確率 確率 2枚の硬貨、3枚の硬貨を投げるときの確率 確率 2つのサイコロを投げるとき 確率 2人のくじ引き 3パターン いろいろな確率 モンティ・ホール問題の説明と実験 指導手順 準備物:紙コップ3個×班、木片1個 ワークシート いろいろな
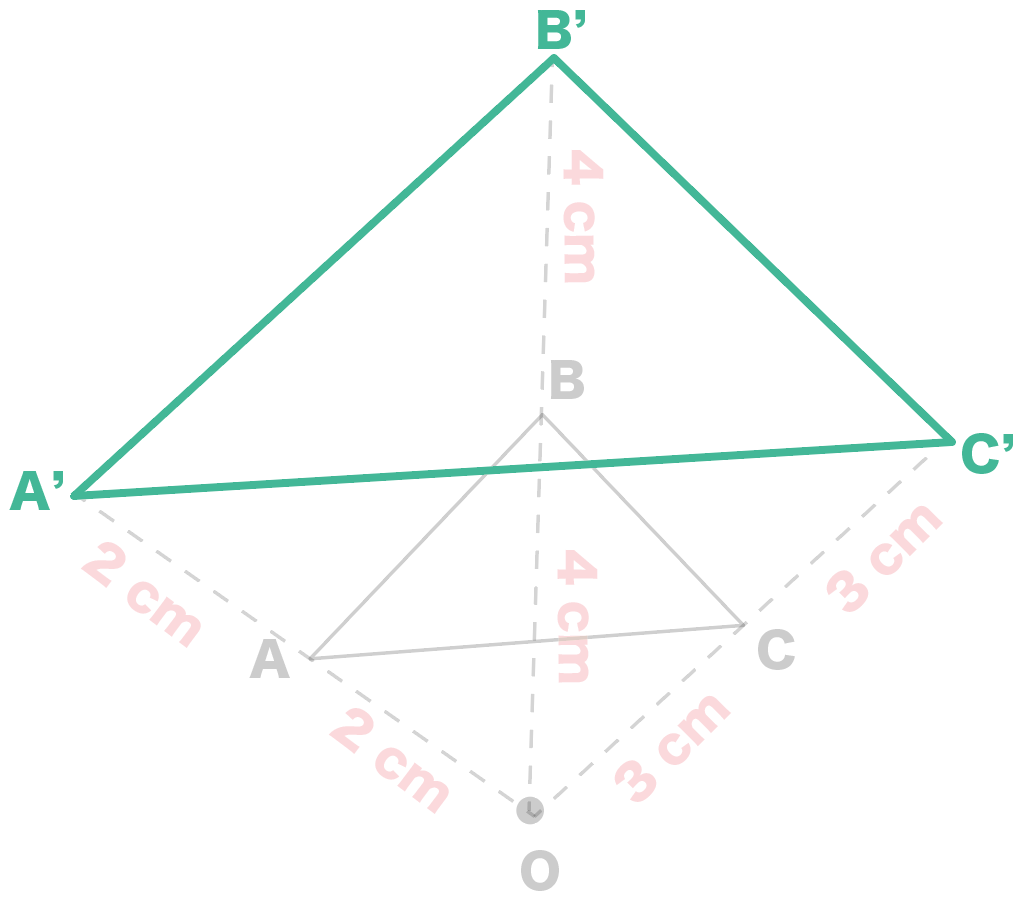



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




相似の中心となる点について 相似の中心となる点についてこんにちは 数学 教えて Goo
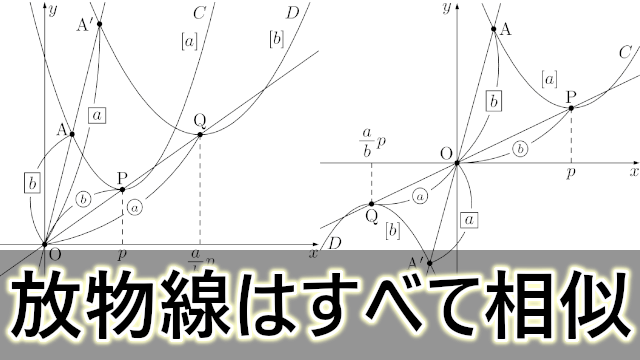
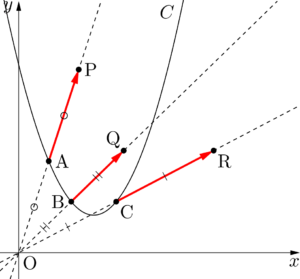
放物線が相似であることの証明 y = a x 2 b x c y=ax^2bxc y = a x 2 b x c のグラフとして表される放物線たちは,強い意味で,すなわち回転を許容しない相似です。 任意の2つの放物線に対して相似の中心が存在して,一方は他方の拡大(縮小)になっています。



Q Tbn And9gcrbotqbxhgpkx6m0pv4nzwika1wmq4gklkertxcpeymmthd6e5v Usqp Cau
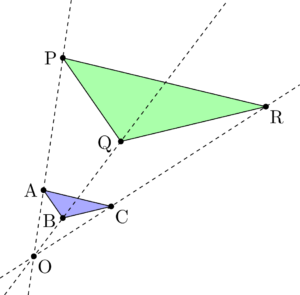



すべての放物線が相似であることの証明 大学入試数学の考え方と解法



中学数学 図形の相似




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear



中学数学 相似とは何か 導入 中学数学の無料オンライン学習サイトchu Su



すべての放物線が相似であることの証明 大学入試数学の考え方と解法




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
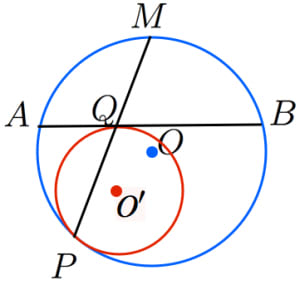



接する2つの円の相似の中心 高校数学の美しい物語




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題




Nitter



Studydoctor平行線と台形 中3数学 Studydoctor




3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
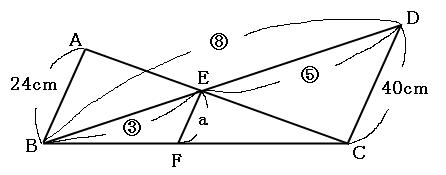



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし
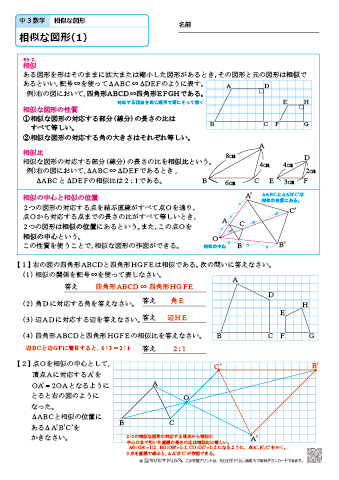



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




相似な図形 計算 台形 練習問題 苦手な数学を簡単に




相似の位置と中心 中3数学 Youtube
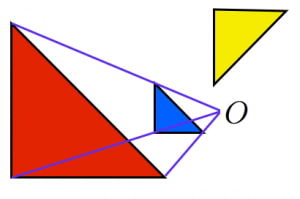



全ての放物線が相似であることの証明 高校数学の美しい物語




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




接する2つの円の相似の中心 高校数学の美しい物語
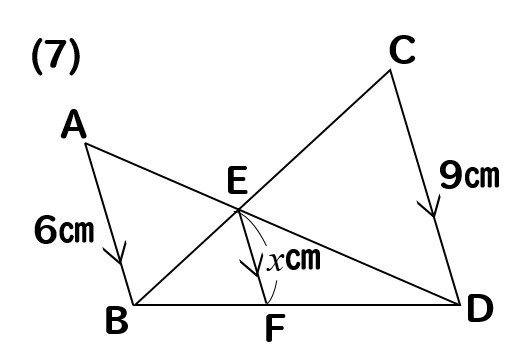



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋
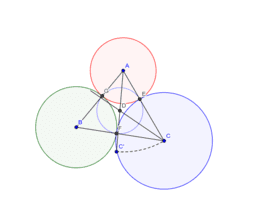



アポロニウスの問題 Geogebra



中学数学 図形の相似



すべての放物線が相似であることの証明 ページ 2 大学入試数学の考え方と解法
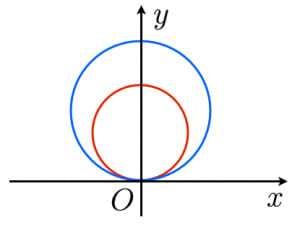



接する2つの円の相似の中心 高校数学の美しい物語




中学数学 よく出る円と相似の融合問題 Pikuu



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
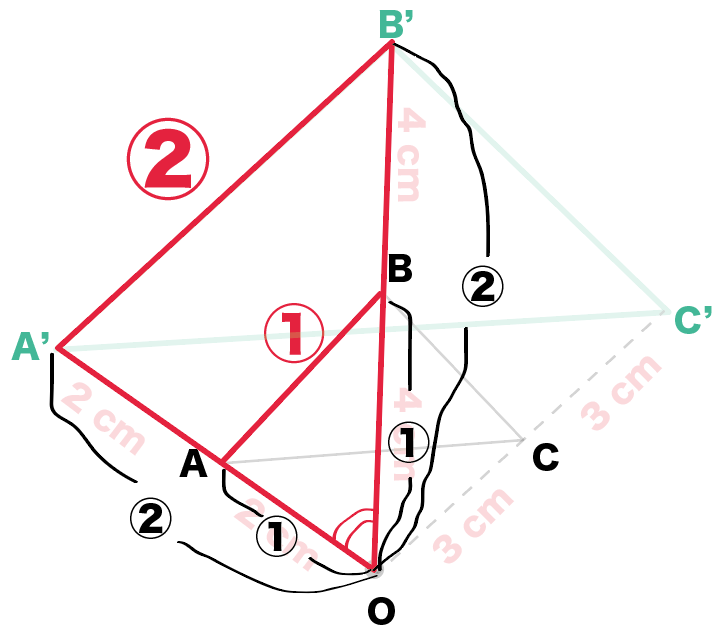



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



平面における変換
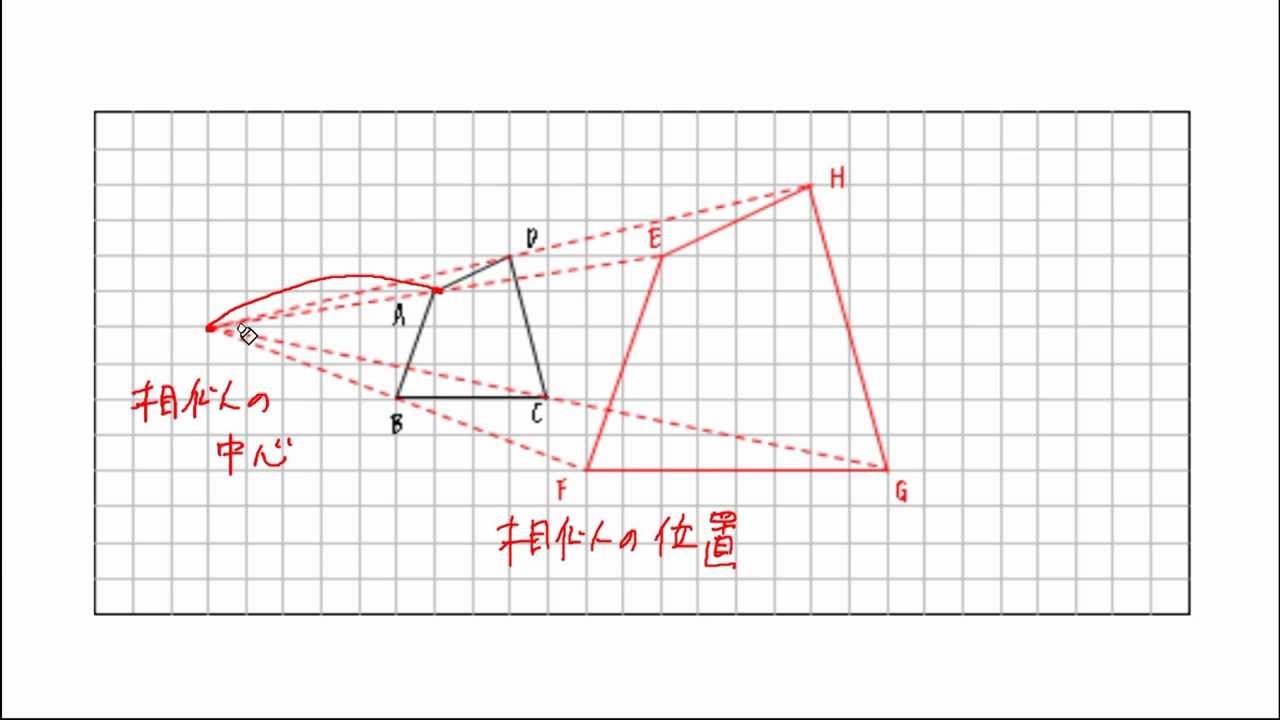



相似の中心と作図 Youtube



Studydoctor相似の位置と中心 中3数学 Studydoctor
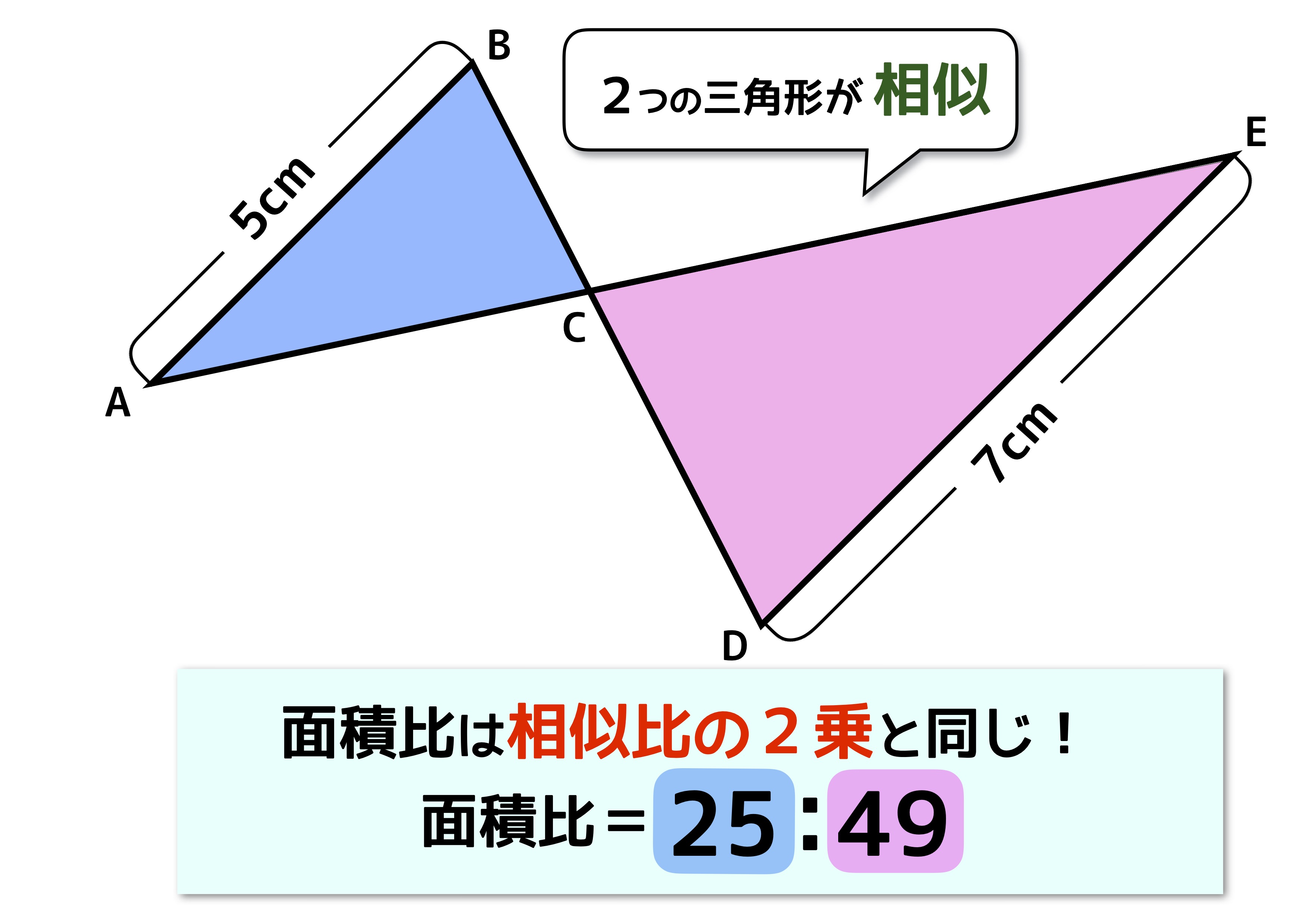



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




中3 相似の中心を利用した作図 Youtube
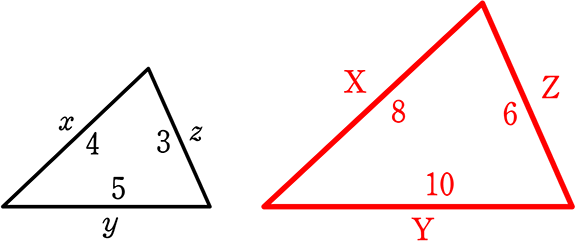



中学数学 図形の相似
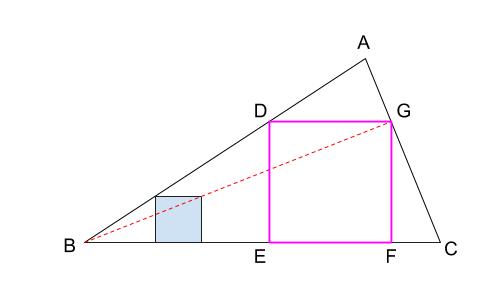



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su
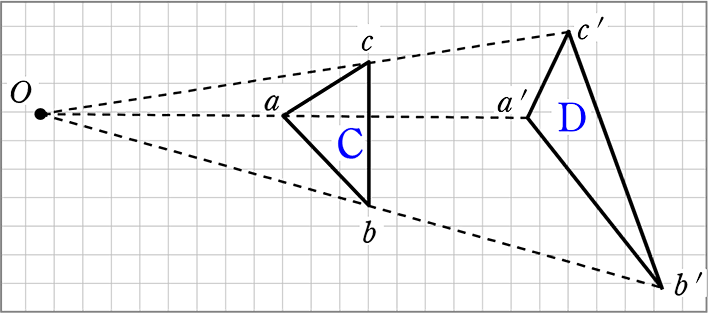



中学数学 図形の相似



中学数学 図形の相似



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor



Http Www Criced Tsukuba Ac Jp Renkei Msa Lessonplan Ooneda 2nd Medio Ooneda07 Jap Pdf



中学生 アーカイブ Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



相似な図形 確認問題 苦手な数学を簡単に




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学



中3の数学です 円の縮図の書き方がわかりません 点oを相似の中心 Yahoo 知恵袋



Http Www Asahikawa Hkd Ed Jp Asahi Els 13 Seien Suugaku30 Pdf




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット



平面における変換
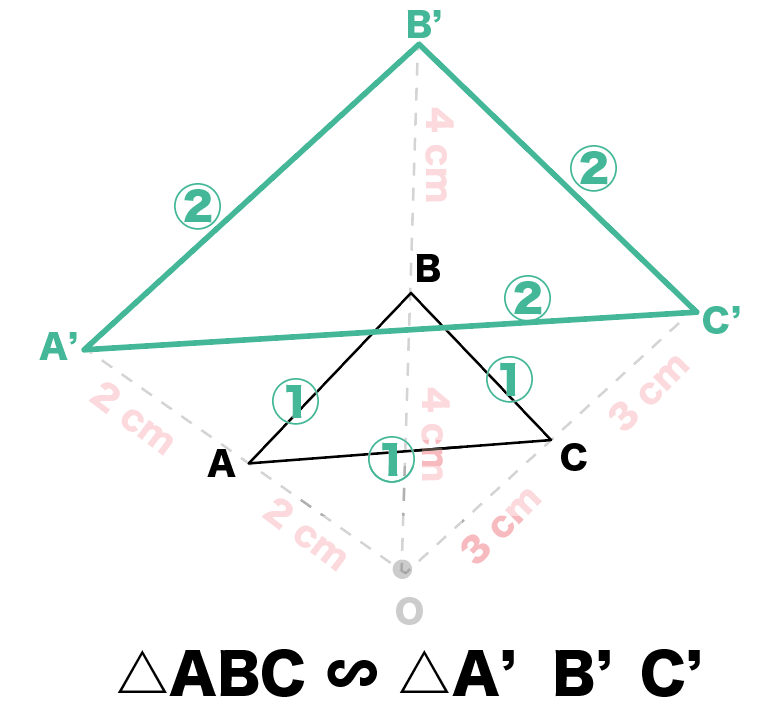



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



相似下の方顔用紙に四角形abcdを点oを相似の中心として 2倍に拡大した四 Yahoo 知恵袋
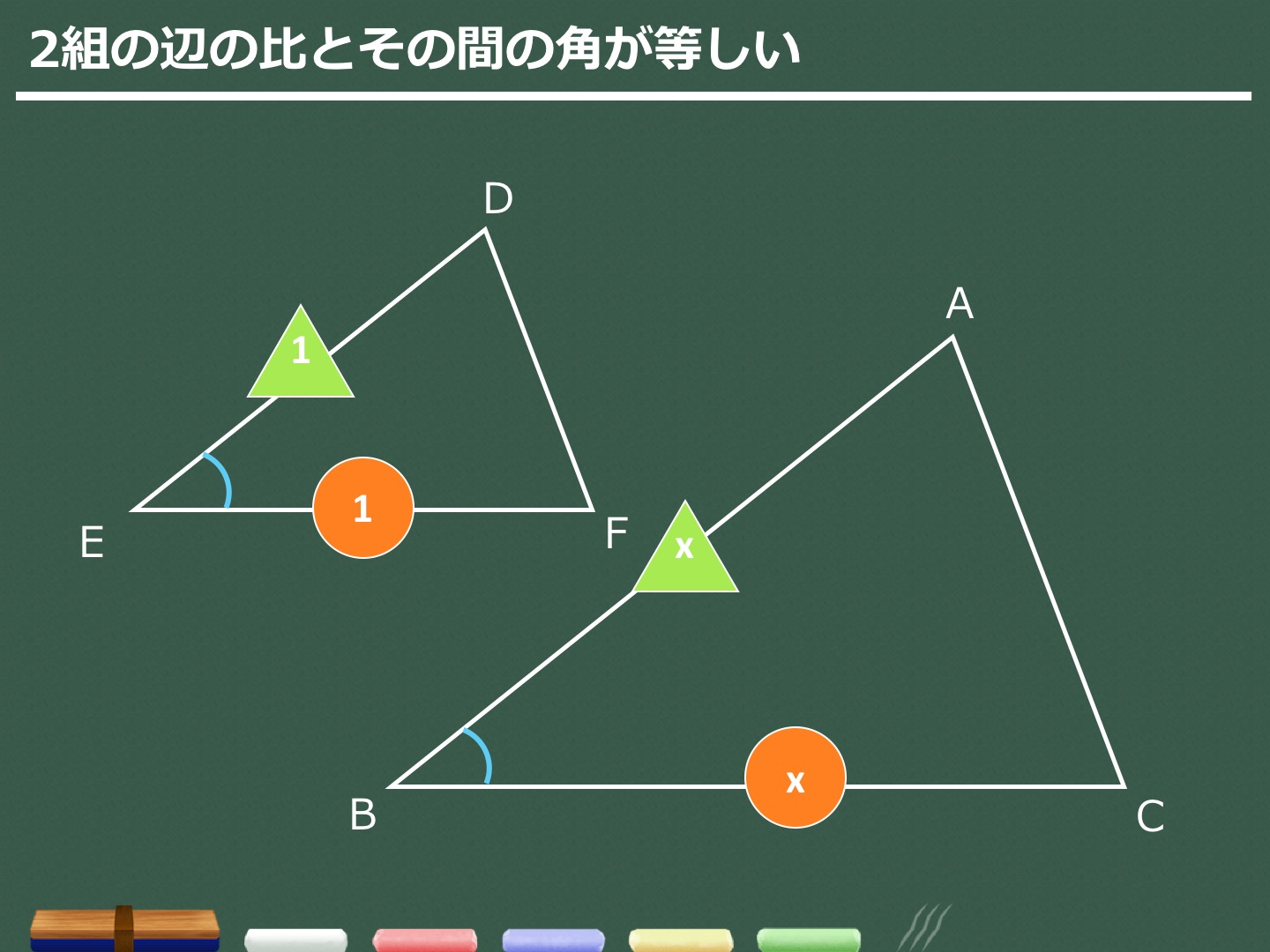



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
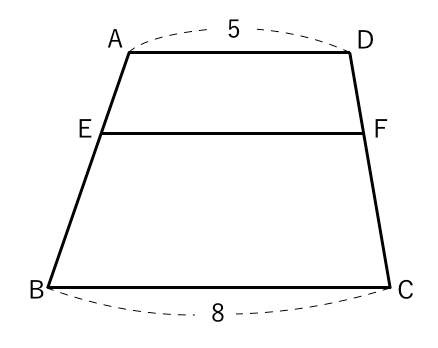



相似な図形 計算 台形 練習問題 苦手な数学を簡単に



図形の相似 規則集3 中学から数学だいすき




中3 相似の中心を利用した作図 Youtube




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座




中学数学 円錐の中心角の求め方 3パターン なぜか分かる はかせちゃんの怪しい研究室




中3 中学3年 数学 相似と比 円周角と中心角 中学生 数学のノート Clear
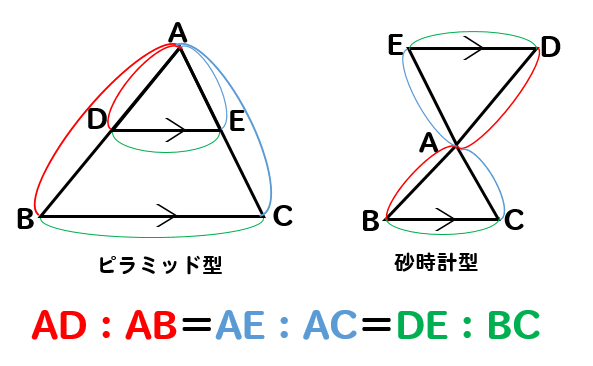



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
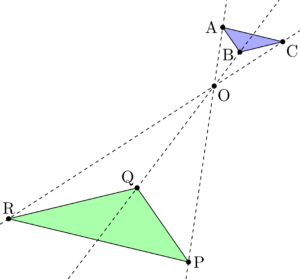



すべての放物線が相似であることの証明 大学入試数学の考え方と解法




相似の中心と作図 Youtube




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学



四角形a B C E は点oを相似の中心として四角形abcdを2分の Yahoo 知恵袋




相似の利用 木の高さを求める方法を問題解説 数スタ




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット
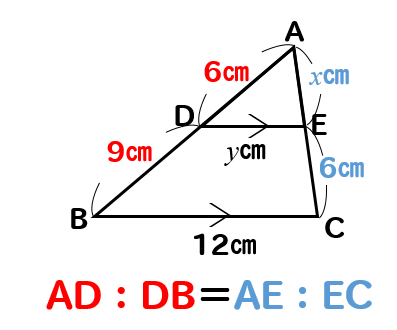



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット




すべての放物線が相似であることの証明 ページ 2 大学入試数学の考え方と解法



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3012 Pdf



相似の中心 中学から数学だいすき




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月




簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




ぬるいパースが描けるようになりたい 共通外接線 共通内接線の描き方




相似の中心と作図 Youtube



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋



Http Www Rs Tottori U Ac Jp Mathedu Mt Xue Sheng Zuo Pin Files J3 Pdf



Http Www Kumamoto Kmm Ed Jp Sugakubraindumps Pdf 3 5 Answer Pdf



数学の相似の図形の問題です分かる方 この問題の答えを教えてくださいこの Yahoo 知恵袋
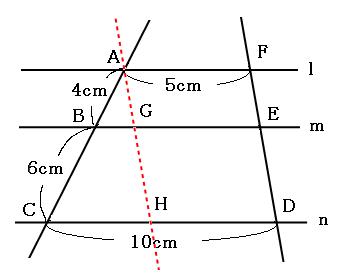



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし




スプリックス 相似の位置と相似の中心 6 Youtube




動画で学習 3 相似の位置 数学



ある図形と相似な図形を作図する時 相似の中心はどこに作っても作図 Yahoo 知恵袋



相似の中心 中学から数学だいすき



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋



平面における変換



1
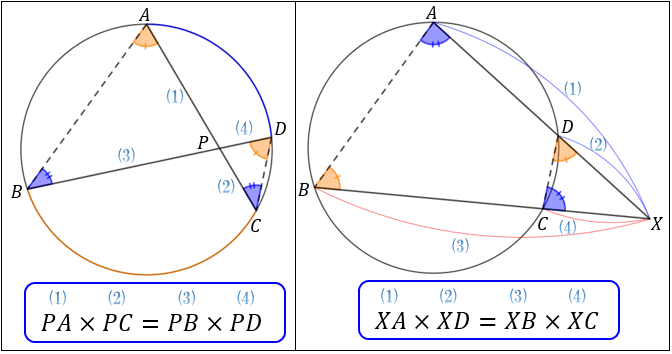



方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ
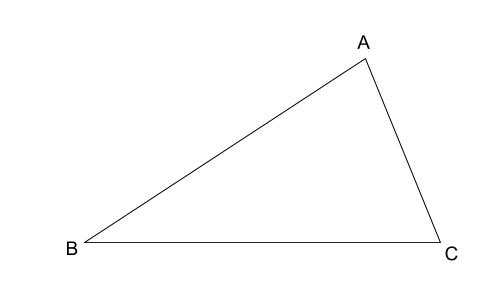



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su



平面における変換



Http Www2 Gsn Ed Jp Houkoku 03c 03c07 03c08s Pdf




相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
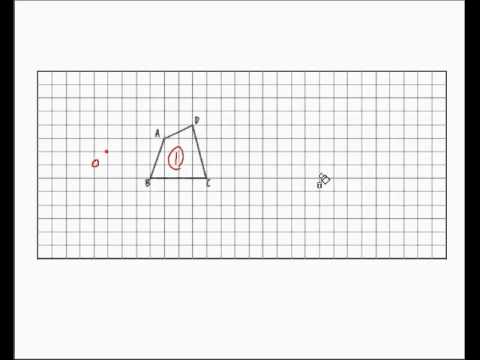



相似の中心と作図 Youtube



中学3年 数学 相似の中心と作図 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



0 件のコメント:
コメントを投稿